α	=	а - b
		a

В результате проведенных исследований и вычислений был получено:

а = 6 378 245 м; b = 6 356 863 м;

α	=	1
		298,3

Поверхность эллипсоида вращения с такими размерами близка к поверхности геоида. В связи с этим такую форму часто называют земным эллипсоидом или земным сфероидом. Такая форма Земли учитывается в геодезии и при изготовлении карт.

Разница между большой и малой полуосями земного сфероида составляет всего 21 382 м. Поэтому для практических целей судовождения Землю часто принимают за шар. Основной единицей длины принятой в судовождении, является морская миля, представляющая собой длину одной минуты дуги меридиана земного шара. Если учитывать, что действительной формой Земли является эллипсоид, то, следовательно, длина одной минуты дуги эллипса не одинакова на всем его протяжении. Так, например, в районе экватора она равна 1861,8 м, а в районе полюса — 1842,9 м; среднеарифметическое их значение приблизительно равно 1852,3 м, что согласуется с длиной одной минуты дуги земного шара.

Так как длина любой окружности равна 2πR, где радиус Земли R равен 6 371 109,7 м, то длина дуги одной минуты земного меридиана будет равна

2πR	=	2 • 3,14 • 6 371 109,7	=	1852,3 м.
360 • 60		360 • 60

В качестве стандартной морской мили в судовождении принято округленное значение длины одной минуты дуги земного меридиана, равное 1852 м (принимая Землю за шар). Кроме того, в судовождении применяются следующие единицы длины:

кабельтов — одна десятая морской мили, применяется в округленном значении—185 м (607 футов);

фут — равен 0,3048 м, или 30,48 см, применяется в основном английских морских картах и в навигационных пособиях для обозначения небольших глубин, а также береговых высот;

ярд — равен 3 футам, или 91,44 см, применяется на английских морских картах и в навигационных пособиях;

морская сажень - равна 6 футам, или 1,83 м, применяется на английских морских картах и в навигационных пособиях при обозначении, больших глубин;

статутная миля (береговая) — равна 5280 футам, или 1609,4 м, и применяется для измерения расстояния при плавании по рекам и озерам, а также на суше.

Основная единица скорости — узел, соответствует одной миле в час, например 15 уз означает 15 миль в час. Узел, как единица скорости, возник в эпоху парусного флота. Скорость судна измерялась при помощи выпускаемого за корму лаглиня с деревянным сектором на конце. Лаглинь разбивался узлами на отрезки, равные 1/120 морской мили. При выпускании лаглиня за борт подсчитывали, сколько узлов пройдет через планширь за период времени, равный 30 с, т. е. за 1/120 ч. Количество таких вытравленных узлов соответствовало скорости судна.

Прямая P_NP_S (рис. 2), вокруг которой Земля совершает свое суточное вращение, называется земной осью; она совпадает с малой осью земного сфероида. Земная ось пересекает поверхность сфероида в точках p_n и p_s, которые называются географическими полюсами. Причем, тот полюс со стороны которого вращение Земли усматривается против часовой стрелки, называют северным (N), противоположный — южным (S).

Если провести через центр Земли горизонтальную и вертикальную плоскости, то на земной поверхности образуются круги, которые .называются большими в отличие от малых, образующихся при пересечении шара плоскостями, не проходящими через его центр. Окружность большого круга ECBQ, образующаяся от пересечения земной поверхности плоскостью, перпендикулярной оси вращения Земли, называется экватором. Экватор делит поверхность земного шара на два полушария — северное и южное. Окружность малого круга aAa₁, плоскость которого параллельна плоскости экватора, называется географической параллелью. Окружности больших кругов P_NQP_SEP_N, проходящие через полюса земной оси, называются географическими меридианами. Меридиан, проходящий через Гринвичскую обсерваторию (вблизи Лондона), называется начальным, или нулевым; он делит поверхность земного шара на две половины — восточную и западную.

§ 2. ГЕОГРАФИЧЕСКИЕ КООРДИНАТЫ МЕСТА

Пусть судно и находящийся на нем наблюдатель расположены в точке А на поверхности Земли (см. рис. 2). Вообразим меридиан и параллель, проходящими через эту точку А и вершины центральных углов АОВ и СОВ.

Широтой φ_а точки А называется центральный угол АОВ, лежащий в плоскости меридиана и измеряемый дугой меридиана ВА, заключенной между экватором и параллелью точки А. В за висимости от того, в каком полушарии лежит точка, широте приписывается наименование северной или южной. Широты отсчитываются от 0 до 90°. Широты всех точек, лежащих на экваторе, равны 0°, а широты полюсов — 90°, или 90°N и 90°S.

Долготой λ_а точки А называется центральный угол СОВ, лежащий в плоскости экватора, который измеряется дугой экваторa CB, заключенной между нулевым меридианом и меридианом точки А. Поскольку нулевой меридиан  делит земной шар на два полушария — западное (вестовое) и восточное (остовое), то в зависимости от наименования полушария, в котором расположена наша точка, долготам приписывается наименование W или O^st. Счет долгот ведется от 0 до 180°. При плавании из пункта отхода А (отшествия) в пункт прихода В (пришествия) судно меняет свою широту и долготу (рис. 3).

Величина, на которую изменяется широта при переходе судна из пункта отшествия φ₁ в пункт пришествия φ₂, называется разностью широт (РШ).

 

РШ измеряется меньшей из дуг меридиана между параллелями пункта отхода А и прихода В в пределах от 0 до 180° и имеет наименование к N, если северная широта увеличивается или южная уменьшается, или к S, если увеличивается южная широта или северная уменьшается.

Если северной широте приписать знак «плюс» (+), а южной — «минус» ( — ), то РШ можно определить по формуле

РШ = φ₂ - φ₁.

Примеры.

1.	—	φ2 = +24º12´	2.	—	φ2 = —64º30´
		φ1 = +16º08´			φ1 = —52º12´
	РШ = +08º04´, или к N			РШ = —12º18´, или к S
3.	—	φ2 = —44º42´	4.	—	φ2 = + 12º32´
		φ1 = + 12º20´			φ1 = —8º16´
	РШ = —57º02´, или к S			РШ = + 20º48´, или к N

Можно также сказать, если широты двух пунктов φ₁ и φ₂ расположены в одном полушарии, то РШ равна их разности, если φ₁ и φ₂ расположены в разных полушариях, то РШ равна их сумме.

Примеры.

1.	—	φ2 = 46º24´N	2.	+	φ2 = 14º28´S
		φ1 = 34º12´N			φ1 = 6º18´N
	РШ = 12º12´к N			РШ = 20º36´ S
3.	+	φ2 = 3º28´N	4.	—	φ2 = 12º36´S
		φ1 = 2º46´S			φ1 = 8º18´S
	РШ = 6º14´ к N			РШ = 4º18´ к S

Разностью долгот (РД) называется величина, на которую изменяется долгота при плавании судна из пункта отшествия λ₁ в пункт пришествия λ₂. Измеряется РД меньшей из дуг экватора между меридианами данных пунктов отхода и прихода в пределах от 0 до 180° и имеет наименование к O^st, если восточная долгота увеличивается или западная уменьшается, и к W, если восточная долгота уменьшается или западная увеличивается.

Если восточной долготе приписать знак «плюс» (+), а западной «минус» (—), то РД можно определить по формуле

РД = λ₂ - λ₁.

При этом сумма долгот может получиться больше 180°. В таком случае полученную сумму вычитаем из 360° и меняем наименование разности долгот.

Примеры.

1.	—	λ2 = + 28º40´	2.	—	λ2 = +152º46´
		λ1 = + 22º08´			λ1 = —148º22´
	РД = + 06º32´, или к Оst			РД = +301º08´ = —58º52´=58º52´ или к W
3.	—	λ2 = —2º19´	4.	—	λ2 = +4º42´
		λ1 = + 1º07´			λ1 = —2º04´
	РД = —3º26´, или к W			РД = + 6º46´, или к Оst

Принято считать, если долготы двух пунктов λ₁ и λ₂ расположены в одном полушарии, то РД равна их разности, а если λ₁ и λ₂ расположены в разных полушариях, то РД равна их сумме.

Примеры. 

1.	—	λ2 = 20º26´ Оst	2.	—	λ2 = 10º12´W
		λ1 = 10º12´ Оst			λ1 = 8º06´W
	РД = 18º14´ к Оst			РД = 2º06´ к W
3.	+	λ2 = 4º42´W	4.	+	λ2 = 84º18´ Оst
		λ1 = 5º02´ Оst			λ1 = 28º12´W
	РД = 9º44´ к W			РД = 112º30´ к Оst

§ 3. ОПРЕДЕЛЕНИЕ НАПРАВЛЕНИЙ В МОРЕ

Через любую точку земной поверхности можно провести отвесную линию или вертикаль zA, которая укажет направление zn — зенит — надир (рис. 4). Горизонтальную плоскость НН', проходящую перпендикулярно отвесной линии и через место наблюдателя точку А, называют плоскостью истинного горизонта наблюдателя. Вертикальную плоскость LL., проходящую через земную ось и место наблюдателя, называют плоскостью истинного меридиана наблюдателя.

Линия пересечения плоскости истинного меридиана наблюдателя с плоскостью истинного горизонта будет называться линией истинного меридиана, т. е. покажет направление линии NS, которая называется полуденной, так как в плоскости LL' солнце бывает точно в полдень.

Вертикальная плоскость КК', перпендикулярная плоскости истинного меридиана наблюдателя, называется плоскостью первого вертикала. Пересечение плоскости первого вертикала с плоскостью истинного горизонта образует на последней направление линии О^stW. Для наблюдателя. Находящегося в любой точке земного шара (за исключением полюсов, где отвесная линия совпадает с осью вращения Земли), линии NS и O^stW указывают на основные стороны света — север, юг, восток, запад — на плоскости истинного горизонта. При этом для наблюдателя, обращенного лицом к северу, справа будет направление на восток, слева — на запад. В судовождении приняты три системы деления горизонта: круговая, четвертная и румбовая. В настоящее время основной является круговая система, которая используется для ведения, прокладки на карте и во всех приборах, указывающих направление.

В круговой системе плоскость истинного горизонта разбита на 360°. За начальное направление принята линия NS, от точки N которой ведется отсчет от 0 до 360° по часовой стрелке. Основным направлениям N, O^st, S, W соответствуют 0, 90, 180, 270°. Круговая система является основной и используется во всех приборах, указывающих направление.

Линии NS и O^stW делят плоскость истинного горизонта на четыре четверти: NО^st, SО^st, NW, SW. В четвертной системе каждая такая четверть разбита на 90° и отсчет ведется от направлений N или S в сторону O^st или W от 0 до 90°. При такой системе деления горизонта направление указывается числом градусов с наименованием четверти. Например, NO^st45°, SW36°. Счет градусов в NО^st и SW четвертях ведется по направлению движения часовой стрелки, а в SО^st и NW четвертях — против часовой стрелки.

Четвертная система применяется обычно при астрономических определениях и при рассмотрении некоторых теоретических вопросов.

Третья система— румбовая (рис. 5)—зародилась еще в эпоху парусного флота. В этой системе каждая четверть горизонта разбита на восемь частей, а весь горизонт на 32 части. Полученные 32 направления называются румбами. Румб представляет собой угол между двумя соседними направлениями, равный ¹/₃₂ части окружности, или 360° : 32 = 11¹/₄°.

Румбы в каждой четверти имеют порядковые номера от 0 до 8 и считаются от N или S в обе стороны. Нумерация румбов в NO^st и SW четвертях идет по движению часовой стрелки, а в SO^st и NW — против движения часовой стрелки. Нулевые и восьмые румбы, т. е. направления на точки N, O^st, S, W, называются главными румбами. Румбы NО^st, SО^st, SW, NW, делящие каждую четверть горизонта пополам, называются четвертными. Вторые и шестые румбы называются трехбуквенными, так как их названия состоят из трех букв — к названию каждой четверти прибавляется название главного ближайшего румба. Вторые румбы: NNО, SSO, SSW, NNW; шестые: ONO, OSO, WSW, WNW. Нечетные румбы составлены из названия главных или четвертных    румбов с прибавлением голландского слова «ten» (тэн),  обозначающего предлог «к», и наименования главного румба, к которому приближается данный нечетный румб (табл. 1), например, NOtO, NWtN, NtO.

 

 

 

 

Таблица 1

 

Номер румба	Наименование румба	Соответствующее число градусов по четвертям	Соответствующее число градусов по круговому счету	Номер румба	Наименование румба	Соответствующее число градусов по четвертям	Соответствующее число градусов по круговому счету
0	N	N    0°	0°	0	S	S  0°	180°
1	NtO	11  1/4	11  1/4	1	StW	11   1/4	191  1/4
2	NNO	22  1/2	22  1/4	2	SSW	22  1/2	202  1/2
3	NOtN	33  3/4	33  3/4	3	SWtS	33  3/4	213  3/4
4	NO	N  0 45	45	4	SW	SW 45	225
5	NOtO	56  1/4	56  1/4	5	SWtW	56  1/4	236  1/4
6	ONO	67  1/2	67  1/2	6	WSW	67  1/2	247  1/2
7	OtN	78  3/4	78  3/4	7	WtS	78  3/4	258  3/4
8	O	0  90	90	8	W	W   90	270
7	OtS	78  3/4	101  1/2	7	WtN	78  3/4	281  1/4
6	OSO	67  1/2	112  1/2	6	WNW	67  1/2	292  1/2
5	SOtO	56  1/4	123  3/4	5	NWtW	56  1/4	303  3/4
4	SO	S  0 45	135	4	NW	NW 45	315
3	SOtS	33  3/4	146  1/4	3	NWtN	33  3/4	326  1/4
2	SSO	22  1/2	157  1/2	2	NNW	22  1/2	337  1/2
1	StO	11  1/4	168  3/4	1	NtW	11  1/4	348  3/4

В настоящее время румбовая система применяется для обозначения направлений ветра, течения или других приближенных направлений. Слово румб сохранилось как термин, обозначающий какое-либо направление на море.

Для перевода направления, данного по четвертному счету, в круговой следует: в первой (NO^st) четверти оставить число градусов без изменения; во второй (SО^st) данное число градусов вычесть из 180°; в третьей (SW) к данному числу градусов прибавить 180°; в четвертой (NW) данное число градусов вычесть из 360°. Наименование четверти при переходе от четвертного счета к круговому не пишется. Например, направлению SO^st 36,0° в круговой системе будет соответствовать направление, равное 144,0°. В судовождении обычно приходится иметь дело с двумя направлениями — направлением движения судна и направлением на какой-либо объект. Направление движения судна может быть определено положением- его диаметральной плоскости по отношению к плоскости истинного меридиана. Угол между нордовой частью плоскости истинного меридиана и носовой частью диаметральной плоскости судна называется истинным курсом (ИК) судна. Направление на какой-либо предмет определяется углом между нордовой частью плоскости истинного меридиана и вертикальной плоскостью, проходящей через место наблюдателя и наблюдаемый предмет, и называется истинным пеленгом (ИП). Истинный пеленг не зависит от направления диаметральной плоскости судна.

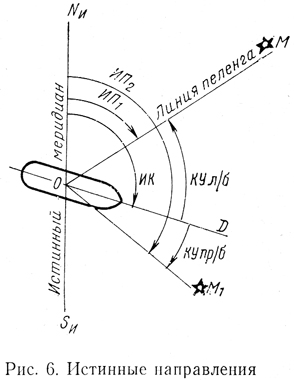
На плоскости истинного горизонта ИК, и ИП изображаются углами, одной стороной которых является истинный меридиан, а второй — или линия курса — след от диаметральной плоскости судна (при определении курса) — или линия пеленга — след вертикальной плоскости, проходящей через место наблюдателя и наблюдаемый объект. Истинные курсы и истинные пеленги отсчитываются от нордовой части истинного меридиана наблюдателя по движению часовой стрелки от 0 до 360°.

Угол между нордовой частью истинного меридиана и направлением с предмета на судно, отличающийся на 180° от истинного пеленга, называется обратным истинным пеленгом (ОИП).

Угол между носовой частью диаметральной плоскости судна и направлением на данный предмет называется курсовым углом (КУ). Курсовые углы отсчитывают от носовой части диаметральной плоскости судна по правому и левому бортам от 0 до 180° (рис. 6).

Из рис. 6 находим:

ИП = ИК + КУ пр/б; ИП = ИК — КУ л/б.

Если в первой формуле ИП получится больше 360°, то из полученной величины надо вычесть 360°. Если во второй формуле ИК<К.У, то к ИК, надо прибавить 360°.

Из формулы ИП=ИК+КУ пр/б можно получить КУ=ИП— ИК. При этом, если результат получится с плюсом, КУ будет правого борта, если с минусом - левого борта.

Если курсовой угол составляет 90° правого или левого борта, он называется траверзом судна. Так и говорят, например, «На траверзе правого борта—маяк». Если в момент траверза ИП=ИК+90°, то наблюдаемый предмет расположен на траверзе правого борта, а если ИП=ИК—90°, то объект расположен на траверзе левого борта.

§ 4. ПОНЯТИЕ О ЗЕМНОМ МАГНЕТИЗМЕ

Наша Земля окружена естественным магнитным полем. Действие магнитных сил обнаруживается как на поверхности Земли, так и в ее недрах и под водой. Все пространство, окружающее земной шар, пронизывается магнитными силовыми линиями, как бы исходящими из магнитного полюса в южном полушарии, огибающими земной шар и входящими в магнитный полюс северного полушария. Условно принято считать, что северный магнитный полюс содержит отрицательный магнетизм, а южный—положительный (рис. 7). В магнитных компасах используется свойство свободно подвешенной намагниченной стрелки устанавливаться вдоль магнитных силовых линий Земли. Такая стрелка своим северным концом указывает на север, а южным—на юг. Магнитные полюсы расположены вблизи географических, но не совпадают с ними. Причем положение магнитных полюсов не остается неизменным, координаты их, хотя и очень медленно, но изменяются.

Магнитное поле Земли в каждой данной точке характеризуется вектором напряженности Т, который называют также полной силой земного магнетизма, и его составляющими. Вектор напряженности всегда направлен по касательным к силовым линиям. Сила земного магнетизма в точке О (рис. 8) изображается вектором OF.

Вертикальная плоскость N_МOZF, в которой расположен вектор OF и ось свободно подвешенной магнитной стрелки, называется плоскостью магнитного меридиана. Плоскость магнитного меридиана составляет с плоскостью истинного меридиана N_ИOZL угол РОН, который называется магнитным склонением d. Магнитное склонение d отсчитывается от северной части истинного меридиана в сторону O^st или W от 0 до 180°. Остовому склонению приписывается знак «плюс», а вестовому — знак «минус».

Например:

d = +3,6°, или d = 3,6°O^st;

d = -2,8°, или d = 2,8°W.

Угол N_MOF между вектором OF и плоскостью истинного горизонта N_ИON_М называется магнитным наклонением Q, которое отсчитывается от горизонтальной плоскости вниз от 0 до 90°. Если опущен северный конец магнитной стрелки, то наклонение положительное, если опущен южный — отрицательное.

Точки на земной поверхности, в которых вектор Т направлен горизонтально, образуют замкнутую линию, дважды пересекающую географический экватор, которая называется магнитным экватором (см. рис. 7).

Если вектор Т разложить на горизонтальную Н и вертикальную Z составляющие в плоскости магнитного меридиана (см. рис. 8), то будем иметь

Н = Т tg Q, Z = T sin Q, или Z = H tg Q.

Величины d, H, Z и Q определяют магнитное поле Земли в данной точке и называются элементами земного магнетизма. Наклонение Q и вертикальная составляющая Z с приближением к магнитным полюсам увеличиваются, а горизонтальная составляющая Н, которая удерживает магнитную стрелку в магнитном меридиане, уменьшается. Отсюда следует, что использование магнитного компаса вблизи полюсов невозможно. Из всех элементов земного магнетизма наиболее важное значение имеет для судовождения магнитное склонение, которое указывается на навигационных морских картах. Однако все элементы земного магнетизма — величины не постоянные, а изменяющиеся. Поэтому на морских навигационных картах, кроме величины магнитного склонения, указывают и год, к которому эта величина склонения относится, а также ее годовое изменение. На морских навигационных картах данные о магнитном склонении наносят или в виде картушки, размещенной на водной поверхности карты, внутри которой приведены сведения о склонении, или указывают только цифрами в тех местах карты, где невозможно разместить картушку. Магнитное склонение, снятое с карты, приводят к году плавания. Для этого рассчитывают его изменение за истекшее время, т. е. величину годового изменения умножают на количество лет, прошедших от года, к которому приведено склонение, до года плавания. Затем па полученную поправку ∆d увеличивают или уменьшают склонение, снятое с карты.

Пример. Плавание происходит в 1975 г. Склонение, снятое с карты, d=9,6°О^st и относится к 1969 г. Годовое увеличение склонения 5'. Привести склонение к году плавания.

Решение. Промежуток времени с 1969 по 1975 г. равен шести годам. Изменение склонения ∆d=6х5=30'=0,5°. Склонение компаса в 1975 г. d = 9,6+0,5 =10,1°.

В некоторых морях значение склонения резко отличается от величины его в близлежащих районах. Резкое отклонение магнитного склонения в какой-либо точке от значения его в окружающих районах называется магнитной аномалией, которое происходит от залежей под поверхностью земли пород, способных намагничиваться. На морских навигационных картах районы магнитных аномалий обводятся сплошными черными жирными линиями, внутри которых показаны возможные колебания магнитного склонения. Там, где границы магнитных аномалий определенны неточно, они обозначаются пунктиром. Незначительные по площади аномалии обозначаются на картах звездочкой, рядом с которой указываются значение и наименование склонения. Иногда наблюдаются внезапные и резкие изменения магнитного поля Земли, называемые магнитными бурями и продолжающиеся от нескольких часов до нескольких дней. Магнитные бури возникают вследствие изменения солнечной активности. При магнитных бурях изменения склонения достигают в умеренных широтах 7°, а в полярных — до 50°. При плавании в районах магнитных аномалий и бурь к показаниям магнитных компасов следует относиться с особой осторожностью.

При известном магнитном склонении в данном районе плавания можно определить положение нордовой части магнитного меридиана относительно нордовой части истинного меридиана, т. е, N_М относительно N_И следовательно, легко можно определить и магнитный курс. Магнитным курсом (МК) называется угол между нордовой частью магнитного меридиана и носовой частью диаметральной плоскости судна; МК отсчитывается по часовой стрелке от 0 до 360°. Угол между нордовой частью магнитного меридиана и направлением на предмет называется магнитным пеленгом (МП), отсчитывается от 0 до 360° (рис. 9). Таким образом, угол N_MOD есть магнитный курс судна, а угол N_MOM магнитный пеленг маяка (М).

Из рис. 9 видно, что истинные курсы и пеленги связаны с магнитными румбами следующими соотношениями:

ИК = МК + d; МК = ИК - d; d = ИК - МК;

ИП = МП + d; МП = ИП - d; d = ИП - МП.

Пример.	ИК = 285°, d = 10,5W			Пример.	МП = 162°, d = 80°Оst
	Рассчитать МК.				Рассчитать ИП.
Решение.	-	ИК = 285°		Решение.	+	МП = 162°
		d = -10,5				d = +8
	МК = 295,5°				ИП = 170°

§ 5. ПОНЯТИЕ О МАГНЕТИЗМЕ СУДОВОГО ЖЕЛЕЗА

Современные суда, имеющие стальной набор корпуса, обшивку, создают собственное магнитное поле. Поэтому на стрелку магнитного компаса, установленного на судне, кроме магнитного поля Земли, будут действовать магнитные поля, создаваемые судовым твердым и мягким в магнитном отношении железом, работой различных электроустановок и т. п.

Под влиянием действия указанных магнитных сил стрелка компаса, установленного на судне, отклонится от магнитного меридиана. Вертикальная плоскость, проходящая через продольную ось подвешенной за центр тяжести стрелки магнитного компаса, установленного на судне, называется плоскостью компасного меридиана. Линия пересечения плоскости истинного горизонта наблюдателя с плоскостью компасного меридиана называется компасным меридианом. Угол в плоскости истинного горизонта наблюдателя между магнитным и компасным меридианами называется девиацией магнитного компаса δ (см. рис. 9). Этот угол отсчитывается от нордовой части магнитного меридиана к O^st или к W от 0 до 180°. Остовой девиации приписывается знак «плюс», вестовой — «минус».

Девиация магнитного компаса не является величиной постоянной и меняется во время плавания судна при изменении курса, широты. Твердое в магнитном отношении судовое железо, намагнитившись, приобретает постоянный магнетизм и действует на картушку магнитного компаса с постоянной относительно судна силой. При изменении судном курса эта сила также меняет свое направление относительно магнитного меридиана и вызывает поэтому на разных курсах неодинаковую по величине и знаку девиацию. Мягкое в магнитном отношении судовое железо при перемене курса перемагничивается, и поэтому на различных курсах оно действует на картушку компаса силой, переменной по величине и направлению, и вызывает неодинаковую девиацию. При изменении судном широты изменяется напряженность магнитного поля Земли и, следовательно, намагниченность мягкого судового железа, что также вызывает изменение девиации. Для уменьшения величины девиации, которая создает неудобства при пользовании магнитным компасом, на судах проводятся работы по уничтожению девиации.

Девиацию уничтожают путем создания в центре компаса магнитных сил, равных по величине, но противоположных по направлению тем силам, которые вызывают девиацию. Это делается установкой постоянных магнитов и так называемого мягкого железа снабжения в виде железных брусков или шаров, размещаемых в непосредственной близости от компаса в специальных приспособлениях. Уничтожение девиации обычно выполняют специалисты — девиаторы, а иногда и судоводители. Однако полностью уничтожить девиацию магнитного компаса нельзя. Поэтому после уничтожения девиации у судовых магнитных компасов определяют остаточную девиацию, которая не должна превышать 2—3°, и составляют таблицу остаточной девиации (табл. 2) для компасных курсов через 10°, начиная с 0°. Для промежуточных курсов δ выбирают простым интерполированием.

Магнитные курсы и пеленги связаны с компасными следующими соотношениями:

МК = КК + δ; КК = МК – δ; δ = МК – КК;

МП = КП + δ; КП = МП – δ; δ = МП – КП.

Таблица 2

КК	δ	КК	δ	КК	δ	КК	δ
0° 10 20 30 40 50 60 70 80	+2,3° +1,7 +1,3 +1,0 +0,5 ±0,0 -0,7 -1,5 -2,0	90° 100 110 120 130 140 150 160 170	-2,7° -3,3 -3,7 -4,0 -4,3 -4,0 -3,7 -3,3 -2,5	180° 190 200 210 220 230 240 250 260	-1,7° -0,7 +0,3 +1,3 +2,0 +2,7 +3,5 +4,0 +4,3	270° 280 290 300 310 320 330 340 350	+4,5° +4,5 +4,3 +4,0 +3,7 +3,5 +3,0 +2,7 +2,5

 

Пример.	КК = 346°, δ = 6°Оst			Пример.	МП = 224,0°; КП = 218,0°
					Рассчитать δ.
Решение.	+	КК = 346°		Решение.	-	МП = 224,0°
		δ = 6°				КП = 218,0°
	МК = 352°				δ = +6,0° = 6,0°Оst

§ 6. ПЕРЕВОД И ИСПРАВЛЕНИЕ РУМБОВ

Установленный на судне компас всегда показывает компасные направления. Однако для ведения прокладки на морской навигационной карте необходимо знать истинные направления: ИК, ИП. Поэтому в судовождении необходимо уметь переходить от компасных направлений к истинным и от истинных к компасным.

Переход от компасного курса (КК) или компасного пеленга (КП) к истинным их значениям называется исправлением румбов, а от истинного курса (ИК) или истинного пеленга (ИП), снятых с карты, к компасным носит название перевода румбов.

Для перевода и исправления румбов необходимо знать общую поправку магнитного компаса, которая является результатом совместного действия сил земного магнетизма и магнитного поля судна и представляет собой алгебраическую сумму склонения и девиации. Общая поправка магнитного компаса ∆МК бывает остовой или вестовой, т. е. имеет знак «плюс» или «минус», в зависимости от того, к осту или весту отклонена северная часть компасного меридиана от северной части истинного меридиана.

Общая поправка компаса, склонение и девиация связаны следующими соотношениями:

∆МК = d + δ; d = ∆МК - δ; δ = ∆МК – d.

Пример.	d = 10°Оst; δ = 3°W.		Рассчитать ∆МК.
Решение.	+	d = +10°
		δ = -3°
	∆МК = +7,0° = 7,0°Оst

Для исправления компасных румбов на истинные сделаем следующие графические построения. На листе бумаги (рис. 10) проводим вертикальную линию компасного меридиана N_КS_K и отмечаем точку О, в которой находится судно. От компасного меридиана отложим по часовой стрелке угол N_KOD, соответствующий КК судна. В соответствии с выбранным из таблицы значением девиации δ через точку О проводим магнитный меридиан N_MS_М. Полученный угол N_МOD будет магнитным курсом судна. Теперь магнитный курс исправляют в истинный. Для этого через точку О проводят истинный меридиан N_ИS_И в соответствии с наименованием и величиной магнитного склонения d, указанного на карте. При этом, если склонение и девиация имеют остовое наименование, магнитный меридиан будет находиться левее компасного, а истинный — левее магнитного. Полученный угол N_ИOD изображает истинный курс судна.

При исправлении румбов используют следующие соотношения:

ИК = КК + ∆МК; ИП = КП + ∆МК, где ∆MK = d + δ.

Пример. КК = 330°; КП = 69°; d = 12°О^st;

             δ = 3,2°О^st. Определить ∆МК, ИК и ИП.

Решение.	1.	+	d = 12°	2.	+	КК = 330°	3.	+	КП = 69°
			δ = 3,2°			∆МК = +15,2°			∆МК = +15,2°
		∆МК = +15,2°			ИК = 345,2°			ИП = 84,2°

Для перевода истинных курсов в компасные поступают следующим образом. На листе бумаги (рис. 11) проводят вертикальную линию истинного меридиана N_ИО через точку О, в которой находится судно, а также линию истинного курса OD.

 

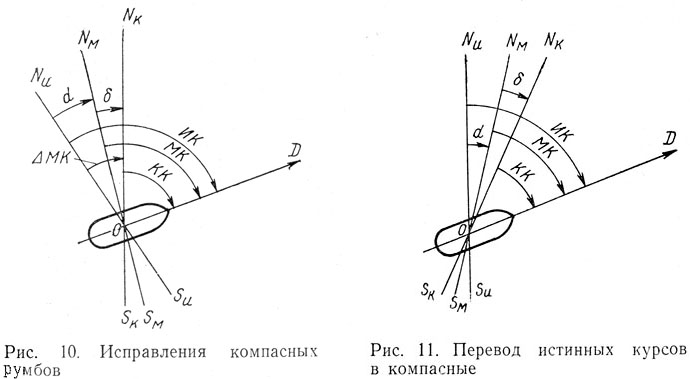
Угол N_ИOD будет истинным курсом. Предположим, что магнитное склонение — остовое. Следовательно, магнитный меридиан N_MО пройдет к востоку от N_И. Таким образом, угол N_МOD будет магнитным курсом судна. Если девиация остовая, то к востоку от N_М проводим компасный меридиан N_KО. В таком случае угол N_KOD — компасный курс судна.

При переводе румбов пользуются следующими соотношениями: MK = ИК – d; КК = МК – δ; КП = ИП - ∆МК.

Пример. ИК = 242°; ИП = 112°; d = 12О^st; δ = 3°О^st. Определить ∆МК, КК и КП.

Решение.	1.	-	ИК = 242°	2.	+	d = +12°	3.	-	ИП = 112°
			d = +12°			δ = +3°			∆МК = 15°
		-	МК = 230°		∆МК = +15°			КП = 97°
			δ = +3°
		КК = 227°

§ 7. ДАЛЬНОСТЬ ВИДИМОСТИ ПРЕДМЕТОВ

В начале этой главы было дано определение истинного горизонта, который является лишь воображаемой плоскостью, так как в море мы наблюдаем видимый горизонт. Наблюдателю, находящемуся на судне в море, представляется, что он находится в центре круга, по окружности которого небесный свод как бы сходится с водной поверхностью. Эта окружность и будет видимым горизонтом наблюдателя. Расстояние от места наблюдателя до линии видимого горизонта называется дальностью видимости горизонта.

Дальность видимости предметов в море определяется наибольшим расстоянием, на котором наблюдатель увидит вершину предмета на линии своего горизонта.

Пусть наблюдатель находится на поверхности Земли в точке В и на высоте е над уровнем моря в точке А расположен глаз наблюдателя (рис. 12). Лучи зрения AC, АС₁, АС₂, AC₃ — касательные к поверхности Земли образуют на ней малый круг, который будет линией теоретического видимого горизонта наблюдателя. Расстояние от места наблюдателя до линии теоретического видимого горизонта, измеряемого по касательной АС, будет называться теоретической дальностью видимого горизонта. Однако действительная дальность видимого горизонта будет больше касательной АС, так как различные слои земной атмосферы имеют различную плотность и проходящий через них луч зрения преломляется. Следовательно, в глаз наблюдателя придет луч не от точки С, а от расположенной за ней точки К, находящейся за линией теоретического видимого горизонта. Наблюдатель будет видеть точку С по касательной АР к действительному пути луча, приподнятой на угол земной рефракции r.

Земная рефракция не является величиной постоянной и зависит от разности температур воды и воздуха, от влажности и присутствия в воздухе пыли. Окружность КК₁ представляет собой линию действительного, или географического, горизонта, а расстояние АК — действительную его дальность. Принято считать, что действительная дальность за счет рефракции увеличивается в среднем на 8% значения теоретической дальности. Действительная, или географическая, дальность видимого горизонта наблюдателя при обычном состоянии атмосферы рассчитывается по формуле

Д_е = 2,08√е,

где Д_е — дальность видимого горизонта, морские мили; е — высота глаза наблюдателя, м.

По этой формуле вычислена таблица 22-а, помещенная в мореходных таблицах МТ-63.

Знание дальности видимости тех или иных предметов в море (маяка, встречного судна) является важным фактором в судовождении и способствует безопасности .мореплавания, точности навигационных определений. Судоводителю важно знать, на каком расстоянии откроется тот или иной предмет (маяк, вершина горы, встречное судно и т. д.). Чем выше предмет, тем, естественно, с большего расстояния его увидит наблюдатель. Наблюдатель, находящийся на судне (рис. 13) с высотой глаза над уровнем моря, равной е, увидит вершину маяка — точку С, имеющего высоту h по касательной к поверхности воды. Следовательно, дальность видимости предметов в море Д_n является суммой дальности видимого горизонта наблюдателя с высотой глаза Д_е и дальности видимого горизонта с высоты предмета Д_h = 2,08√_hм, или Д_п = Д_е + Д_h= 2,08√_е + 2,08√_h = 2,08(√_e+√_h).

Из табл. 22-а МТ-63, войдя в нее со значениями е и h, находят значения Д_е и Д_h в морских милях, сложив которые получают расстояние Д_n.

Для приближенного расчета дальности видимости предметов применяют номограмму Струйского (рис. 14). В этом случае на двух крайних шкалах номограммы отмечают точки, соответствующие высоте глаза наблюдателя и высоте предмета, затем проводят через них прямую и на пересечении этой прямой со средней шкалой получают дальность видимости предмета.

Пример. Найти дальность видимости предмета высотой над уровнем моря h = 26,5м (86 футов) при высоте глаза наблюдателя над уровнем моря е = 4,5 (15 футов).

Решение. Дальность видимости Д_п=15,1 мили, как показано на рис. 14 пунктиром.

На морских картах, в лоциях и других навигационных пособиях указывается дальность видимости маяков и огней для высоты глаза наблюдателя, равной 5 м (Д_к —дальность видимости на карте).

Если высота глаза иная, то вводится поправка (см. рис. 13) Д_n = Д_к+∆Д_к, а для советских карт ∆Д_к=Д_е—Д_5м. Фактическая дальность обнаружения предмета отличается от вычисленной в зависимости от состояния атмосферы.

Пример. Дальность видимости маяка, указанная на карте, Д_к= 20 милям. С какого расстояния увидит огонь наблюдатель, глаз которого находится на высоте е = 16м.

Решение.	-	Де = 8,3 (из табл.22-а)
		Д5 = 4,7 (величина постоянная)
		∆Дк = +3,6
		Дк = 20 (с карты)
	Дn = 23,6 мили